Density Varies Continuously With Respect to Dynamics Uniformly Expanding Maps
Article contents
- Abstract
- References
Abstract
We consider random perturbations of discrete-time dynamical systems. We give sufficient conditions for the stochastic stability of certain classes of maps, in a strong sense. This improves the main result in Alves and Araújo [Random perturbations of non-uniformly expanding maps. Astérisque286 (2003), 25–62], where the stochastic stability in the 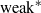 $\mathrm {weak}^*$ topology was proved. Here, under slightly weaker assumptions on the random perturbations, we obtain a stronger version of stochastic stability: convergence of the density of the stationary measure to the density of the Sinai–Ruelle–Bowen (SRB) measure of the unperturbed system in the
$\mathrm {weak}^*$ topology was proved. Here, under slightly weaker assumptions on the random perturbations, we obtain a stronger version of stochastic stability: convergence of the density of the stationary measure to the density of the Sinai–Ruelle–Bowen (SRB) measure of the unperturbed system in the 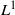 $L^1$ -norm. As an application of our results, we obtain strong stochastic stability for two classes of non-uniformly expanding maps. The first one is an open class of local diffeomorphisms introduced in Alves, Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math.140 (2000), 351–398] and the second one is the class of Viana maps.
$L^1$ -norm. As an application of our results, we obtain strong stochastic stability for two classes of non-uniformly expanding maps. The first one is an open class of local diffeomorphisms introduced in Alves, Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math.140 (2000), 351–398] and the second one is the class of Viana maps.
- Type
- Research Article
- Copyright
-
Copyright © 2012 Cambridge University Press
Access options
Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)
References
[Al00] Alves, J. F. . SRB measures for non-hyperbolic systems with multidimensional expansion. Ann. Scient. Éc. Norm. Sup., 4 e série 33 (2000), 1–32.Google Scholar
[Al03] Alves, J. F. . Statistical analysis of non-uniformly expanding dynamical systems, 24th Braz. Math. Colloq., IMPA, Rio de Janeiro, 2003.Google Scholar
[Al04] Alves, J. F. . Strong statistical stability of non-uniformly expanding maps. Nonlinearity 17(4) (2004), 1193–1215.CrossRefGoogle Scholar
[AA03] Alves, J. F. and Araújo, V. . Random perturbations of non-uniformly expanding maps. Astérisque 286 (2003), 25–62.Google Scholar
[AAV07] Alves, J. F. , Araújo, V. and Vásquez, C. H. . Stochastic stability of non-uniformly hyperbolic diffeomorphisms. Stoch. Dyn. 7(3) (2007), 299–333.CrossRefGoogle Scholar
[ABV00] Alves, J. F. , Bonatti, C. and Viana, M. . SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.CrossRefGoogle Scholar
[ALP05] Alves, J. F. , Luzzatto, S. and Pinheiro, V. . Markov structures and decay of correlations for non-uniformly expanding dynamical systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(6) (2005), 817–839.CrossRefGoogle Scholar
[AV02] Alves, J. F. and Viana, M. . Statistical stability for robust classes of maps with non-uniform expansion. Ergod. Th. & Dynam. Sys. 22 (2002), 1–32.CrossRefGoogle Scholar
[Ara00] Araújo, V. . Attractors and time averages for random maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 17 (2000), 307–369.CrossRefGoogle Scholar
[Ba97] Baladi, V. . Correlation spectrum of quenched and annealed equilibrium states for random expanding maps. Commun. Math. Phys. 186 (1997), 671–700.CrossRefGoogle Scholar
[BBM02] Baladi, V. , Benedicks, M. and Maume-Deschamps, V. . Almost sure rates of mixing for i.i.d. unimodal maps. Ann. Scient. Éc. Norm. Sup., 4 e série 35 (2002), 77–126.Google Scholar
[BBM10] Baladi, V. , Benedicks, M. and Maume-Deschamps, V. . Correcting the proof of Theorem 3.2 in Almost sure rates of mixing for i.i.d. unimodal maps. Ann. E.N.S. (2002), arXiv:1008.5165 (2010).Google Scholar
[BKS96] Baladi, V. , Kondah, A. and Schmitt, B. . Random correlations for small perturbations of expanding maps. Random Comput. Dynam. 4 (1996), 179–204.Google Scholar
[BaV96] Baladi, V. and Viana, M. . Strong stochastic stability and rate of mixing for unimodal maps. Ann. Scient. Éc. Norm. Sup., 4 e série 29 (1996), 483–517.Google Scholar
[BaY93] Baladi, V. and Young, L.-S. . On the spectra of randomly perturbed expanding maps. Comm. Math. Phys 156 (1993), 355–385; Erratum, Comm. Math. Phys. 166 (1994), 219–220.CrossRefGoogle Scholar
[BeC85] Benedicks, M. and Carleson, L. . On iterations of ![]() $1-ax^2$ on (
$1-ax^2$ on ( ![]() $-1, 1$ ). Ann. of Math. (2) 122 (1985), 1–25.CrossRefGoogle Scholar
$-1, 1$ ). Ann. of Math. (2) 122 (1985), 1–25.CrossRefGoogle Scholar
[BeC91] Benedicks, M. and Carleson, L. . The dynamics of the Hénon map. Ann. of Math. (2) 133 (1991), 73–169.CrossRefGoogle Scholar
[BeV06] Benedicks, M. and Viana, M. . Random perturbations and statistical properties of Hénon-like maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(5) (2006), 713–752.CrossRefGoogle Scholar
[BeY92] Benedicks, M. and Young, L.-S. . Absolutely continuous invariant measures and random perturbations for certain one-dimensional maps. Ergod. Th. & Dynam. Sys. 12 (1992), 13–37.CrossRefGoogle Scholar
[Bo75] Bowen, R. . Equilibrium States and the Ergodic Theory of Axiom A Diffeomorphisms (Lecture Notes in Mathematics, 480). Springer, 1975.CrossRefGoogle Scholar
[BR75] Bowen, R. and Ruelle, D. . The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.CrossRefGoogle Scholar
[CE80] Collet, P. and Eckmann, J. . On the abundance of aperiodic behavior for maps on the interval. Comm. Math. Phys. 73 (1980), 115–160.CrossRefGoogle Scholar
[CY05] Cowieson, W. and Young, L.-S. . SRB measures as zero-noise limits. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1091–1113.CrossRefGoogle Scholar
[Ja81] Jakobson, M. . Absolutely continuous invariant measures for one parameter families of one-dimensional maps. Comm. Math. Phys. 81 (1981), 39–88.CrossRefGoogle Scholar
[KK86] Katok, A. and Kifer, Y. . Random perturbations of transformations of an interval. J. Anal. Math. 47 (1986), 193–237.CrossRefGoogle Scholar
[Ki86] Kifer, Y. . Ergodic Theory of Random Perturbations. Birkhäuser, Boston, Basel, 1986.CrossRefGoogle Scholar
[Ki88] Kifer, Y. . Random Perturbations of Dynamical Systems. Birkhäuser, Boston, Basel, 1988.CrossRefGoogle Scholar
[KS69] Krzyzewski, K. and Szlenk, W. . On invariant measures for expanding differentiable mappings. Stud. Math. 33 (1969), 83–92.Google Scholar
[LQ95] Liu, P.-D. and Qian, M. . Smooth Ergodic Theory of Random Dynamical Systems. Springer, Heidelberg, 1995.CrossRefGoogle Scholar
[Me00] Metzger, R. J. . Stochastic stability for contracting Lorenz maps and flows. Commun. Math. Phys. 212 (2000), 277–296.CrossRefGoogle Scholar
[Oh83] Ohno, T. . Asymptotic behaviors of dynamical systems with random parameters. Publ. RIMS Kyoto Univ. 19 (1983), 83–98.CrossRefGoogle Scholar
[Pa00] Palis, J. . A global view of dynamics and a conjecture on the denseness of finitude of attractors. Astérisque 261 (2000), 335–347.Google Scholar
[Ru76] Ruelle, D. . A measure associated with Axiom A attractors. Amer. Jour. Math. 98 (1976), 619–654.CrossRefGoogle Scholar
[Si72] Sinai, Y. . Gibbs measures in ergodic theory. Russ. Math. Surv. 27(4) (1972), 21–69.CrossRefGoogle Scholar
[Vi97] Viana, M. . Multidimensional non-hyperbolic attractors. Publ. Math. IHES 85 (1997), 63–96.CrossRefGoogle Scholar
[Yo86] Young, L.-S. . Stochastic stability of hyperbolic attractors. Ergod. Th. & Dynam. Sys. 6 (1986), 311–319.CrossRefGoogle Scholar
[Yo99] Young, L.-S. . Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.CrossRefGoogle Scholar
[Yo02] Young, L.-S. . What are SRB measures, and which dynamical systems have them?J. Stat. Phys. 108(5) (2002), 733–754.CrossRefGoogle Scholar
wilkinsonfookistand.blogspot.com
Source: https://www.cambridge.org/core/journals/ergodic-theory-and-dynamical-systems/article/strong-stochastic-stability-for-nonuniformly-expanding-maps/FE1F2A44B4DDDA60F0E5A00E2D6C121A
0 Response to "Density Varies Continuously With Respect to Dynamics Uniformly Expanding Maps"
ارسال یک نظر